Right Triangle Angles, Pythagorean Theorem, Unit Circle, Trigonometric Ratios, and the Relationship Between Degrees and Radians

1. What Is Trigonometry?

Trigonometry is a branch of mathematics that studies the relationships between angles and sides of triangles. It has wide applications in physics, engineering, astronomy, and computer science.

2. Right Triangle and Its Angles

A Right Triangle is a triangle in which one angle is equal to 90 degrees.

• One right angle (90°)
• Two acute angles whose sum is 90°

3. Pythagorean Theorem

The Pythagorean Theorem describes the relationship between the sides of a right triangle.

a² + b² = c²

Here, c represents the hypotenuse, while a and b are the legs of the triangle.

4. Trigonometric Ratios

In a right triangle, specific ratios between sides and angles are defined as Trigonometric Ratios.

• sin θ = Opposite / Hypotenuse
• cos θ = Adjacent / Hypotenuse
• tan θ = Opposite / Adjacent

5. Relationships Between Trigonometric Ratios

Important identities exist between trigonometric ratios that are widely used in problem solving.

sin²θ + cos²θ = 1

tan θ = sin θ / cos θ

6. Unit Circle

The Unit Circle is a circle with a radius of 1 that is used to define trigonometric functions for all angles.

On the unit circle:

• The x-coordinate represents cos θ
• The y-coordinate represents sin θ

7. Degrees and Radians

Degrees and Radians are two units used to measure angles.

• One full circle = 360 degrees
• One full circle = 2π radians

8. Converting Between Degrees and Radians

Radians = Degrees × π / 180

Degrees = Radians × 180 / π

9. Relationship Between Angles, Radians, and the Unit Circle

In the Unit Circle, the angle measured in Radians is equal to the length of the arc subtended by that angle.

This relationship makes trigonometric calculations in advanced mathematics more accurate and efficient.

Conclusion

Trigonometry forms the foundation of many mathematical and scientific concepts. Understanding Right Triangles, the Pythagorean Theorem, Trigonometric Ratios, the Unit Circle, and the relationship between Degrees and Radians is essential for solving mathematical problems and real-world applications.

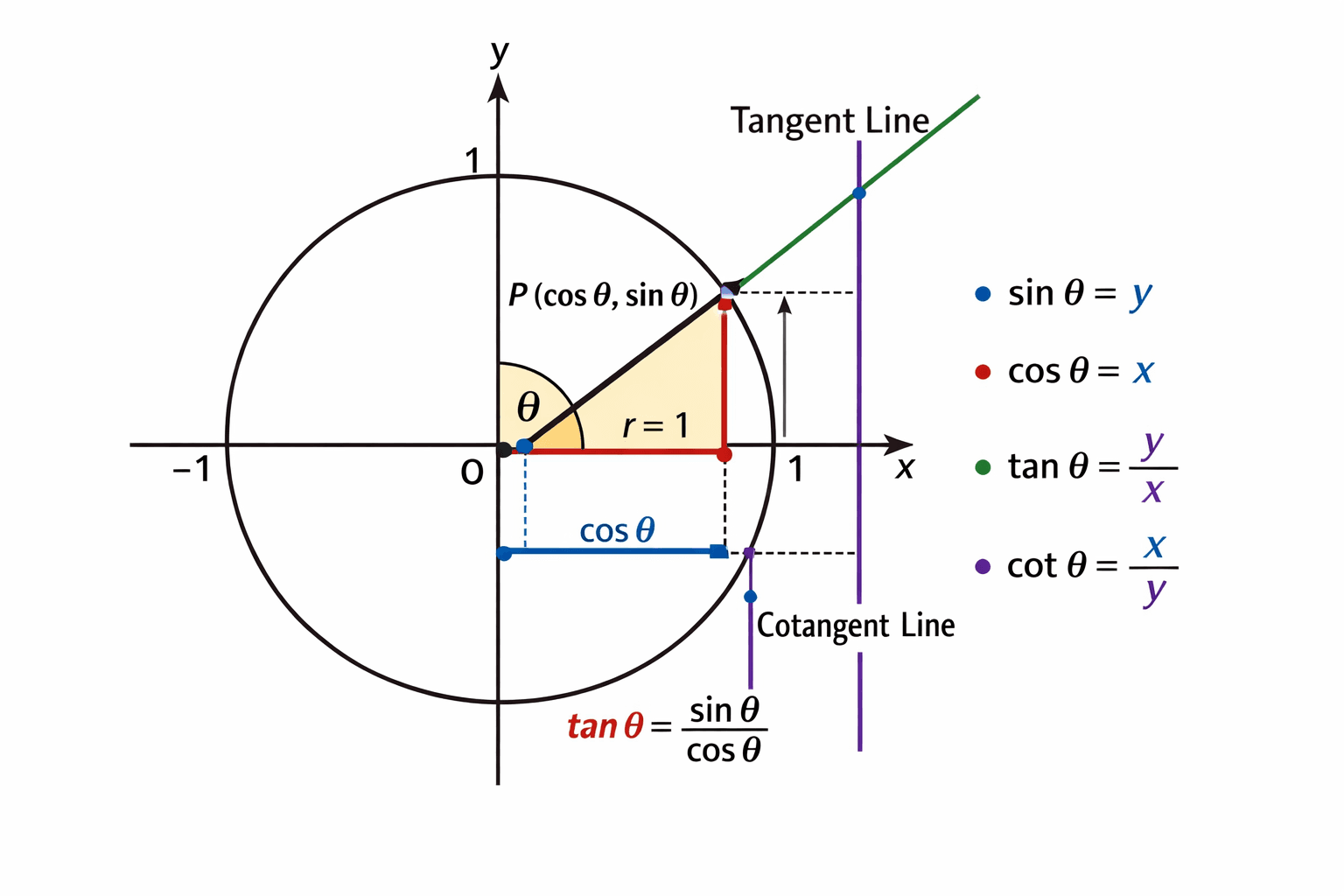
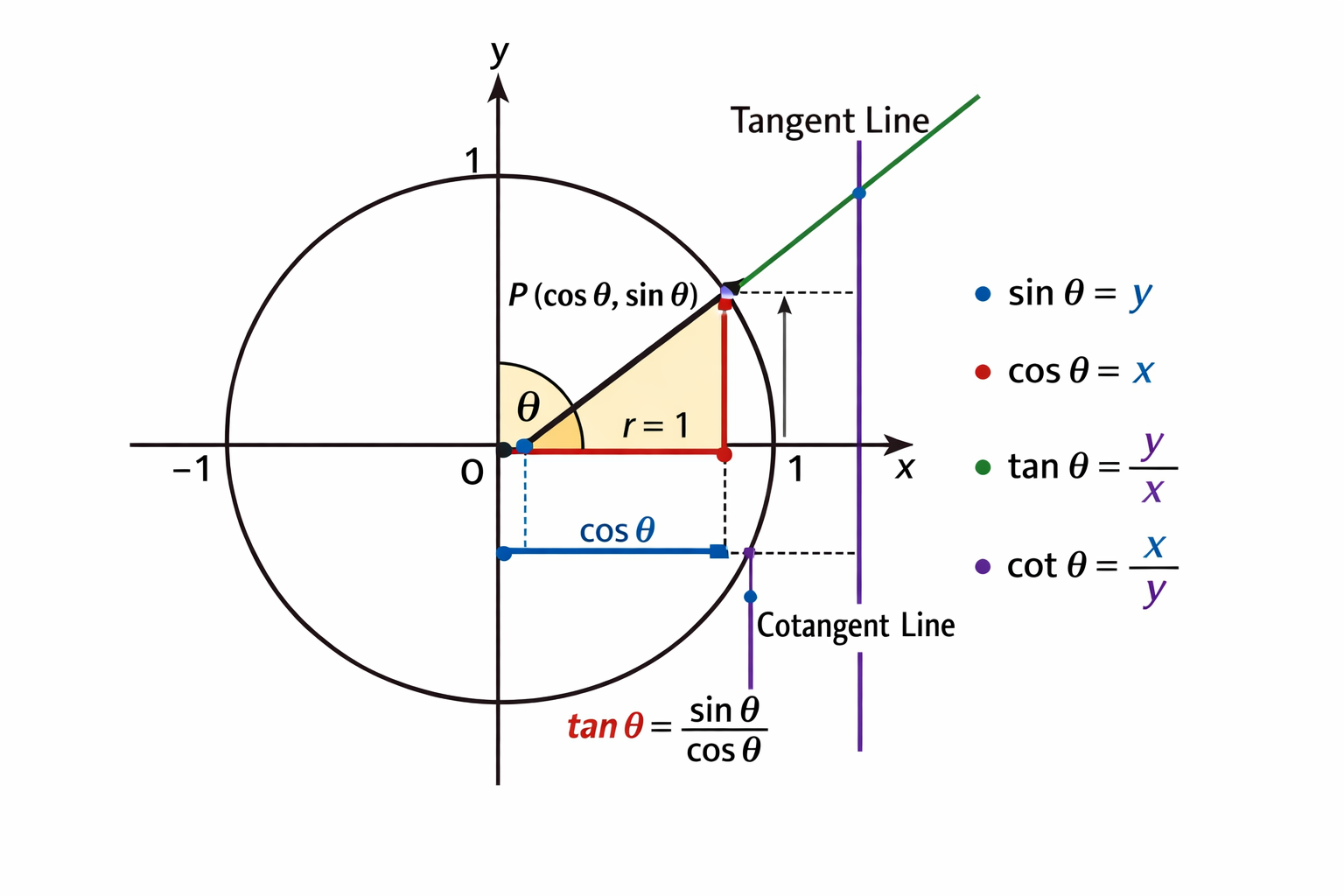
1. What Is the Unit Circle?

The Unit Circle is a circle with a radius equal to 1 and its center located at the origin O(0,0).

This circle is the foundation for defining all Trigonometric Ratios and is widely used in mathematics.

Every point on the unit circle can be described using an angle called θ (theta).

2. How Is Angle θ Defined?

The angle θ starts from the positive x-axis and rotates in the counterclockwise direction.

The rotation continues until the radius reaches a point on the unit circle.

The angle θ can have any value, such as 0°, 30°, 45°, 90°, or even values greater than 360°.

3. Point P on the Unit Circle

The point where the radius meets the unit circle is called point P.

The coordinates of point P are defined as follows:

P(cos θ , sin θ)

This means:

• The horizontal coordinate x equals cos θ
• The vertical coordinate y equals sin θ

This relationship is the most important concept in the unit circle.

4. Sine and Cosine on the Unit Circle

On the unit circle, the sine and cosine values are directly obtained from the coordinates of point P.

Sine (sin θ):

sin θ represents the vertical distance of point P from the x-axis.

sin θ = y

Cosine (cos θ):

cos θ represents the horizontal distance of point P from the y-axis.

cos θ = x

5. Tangent (tan θ)

The tangent function is defined as the ratio of sine to cosine:

tan θ = sin θ / cos θ

Geometrically, tangent is represented on the line that is tangent to the unit circle.

This tangent line passes through the point where the radius intersects the circle, and its length represents the value of tan θ.

When cos θ = 0 (for example, at 90°), the tangent function is undefined.

6. Cotangent (cot θ)

The cotangent function is the reciprocal of tangent and is defined as:

cot θ = cos θ / sin θ

Cotangent is represented on a vertical tangent line, and its length corresponds to the value of cot θ.

When sin θ = 0 (for example, at 0°), the cotangent function is undefined.

Conclusion

The Unit Circle is the core tool for understanding trigonometry. By mastering angle θ, point P, and their relationship with sin, cos, tan, and cot, students can develop a strong conceptual foundation for advanced trigonometric topics.