زوایای مثلث قائم‌الزاویه، قضیه فیثاغورس، دایره مثلثاتی، نسبت‌های مثلثاتی و ارتباط درجه و رادیان

1. مثلثات چیست؟

مثلثات شاخه‌ای از ریاضیات است که به بررسی ارتباط بین زاویه‌ها و اضلاع مثلث می‌پردازد و کاربرد گسترده‌ای در فیزیک، مهندسی و نجوم دارد.

2. مثلث قائم‌الزاویه و زوایای آن

مثلث قائم‌الزاویه مثلثی است که یکی از زوایای آن برابر با 90 درجه است.

• یک زاویه قائمه (90 درجه)
• دو زاویه تند که مجموع آن‌ها 90 درجه است

3. قضیه فیثاغورس

قضیه فیثاغورس رابطه‌ای بین اضلاع مثلث قائم‌الزاویه برقرار می‌کند.

a² + b² = c²

در این رابطه، c وتر و a و b اضلاع قائم هستند.

4. نسبت‌های مثلثاتی

در مثلث قائم‌الزاویه، نسبت‌های خاصی بین اضلاع و زوایا تعریف می‌شود که به آن‌ها نسبت‌های مثلثاتی می‌گویند.

• sin θ = ضلع مقابل / وتر
• cos θ = ضلع مجاور / وتر
• tan θ = ضلع مقابل / ضلع مجاور

5. روابط بین نسبت‌های مثلثاتی

بین نسبت‌های مثلثاتی روابط مهمی وجود دارد که در حل مسائل کاربرد فراوان دارند.

sin²θ + cos²θ = 1

tan θ = sin θ / cos θ

6. دایره مثلثاتی

دایره مثلثاتی یا Unit Circle دایره‌ای با شعاع 1 است که برای تعریف نسبت‌های مثلثاتی تمامی زوایا استفاده می‌شود.

در دایره مثلثاتی:

• مختصات x برابر cos θ
• مختصات y برابر sin θ

7. درجه و رادیان

درجه و رادیان دو واحد اندازه‌گیری زاویه هستند.

• یک دور کامل دایره = 360 درجه
• یک دور کامل دایره = 2π رادیان

8. تبدیل درجه به رادیان و بالعکس

رادیان = درجه × π / 180

درجه = رادیان × 180 / π

9. ارتباط زاویه، رادیان و دایره مثلثاتی

در دایره مثلثاتی، اندازه زاویه بر حسب رادیان برابر با طول کمان مقابل آن زاویه است.

این ارتباط باعث می‌شود محاسبات مثلثاتی در ریاضیات پیشرفته ساده‌تر و دقیق‌تر شوند.

نتیجه‌گیری

مثلثات پایه بسیاری از مفاهیم ریاضی و علمی است. درک مثلث قائم‌الزاویه، قضیه فیثاغورس، نسبت‌های مثلثاتی، دایره مثلثاتی و ارتباط درجه و رادیان نقش مهمی در حل مسائل ریاضی و کاربردهای علمی دارد.

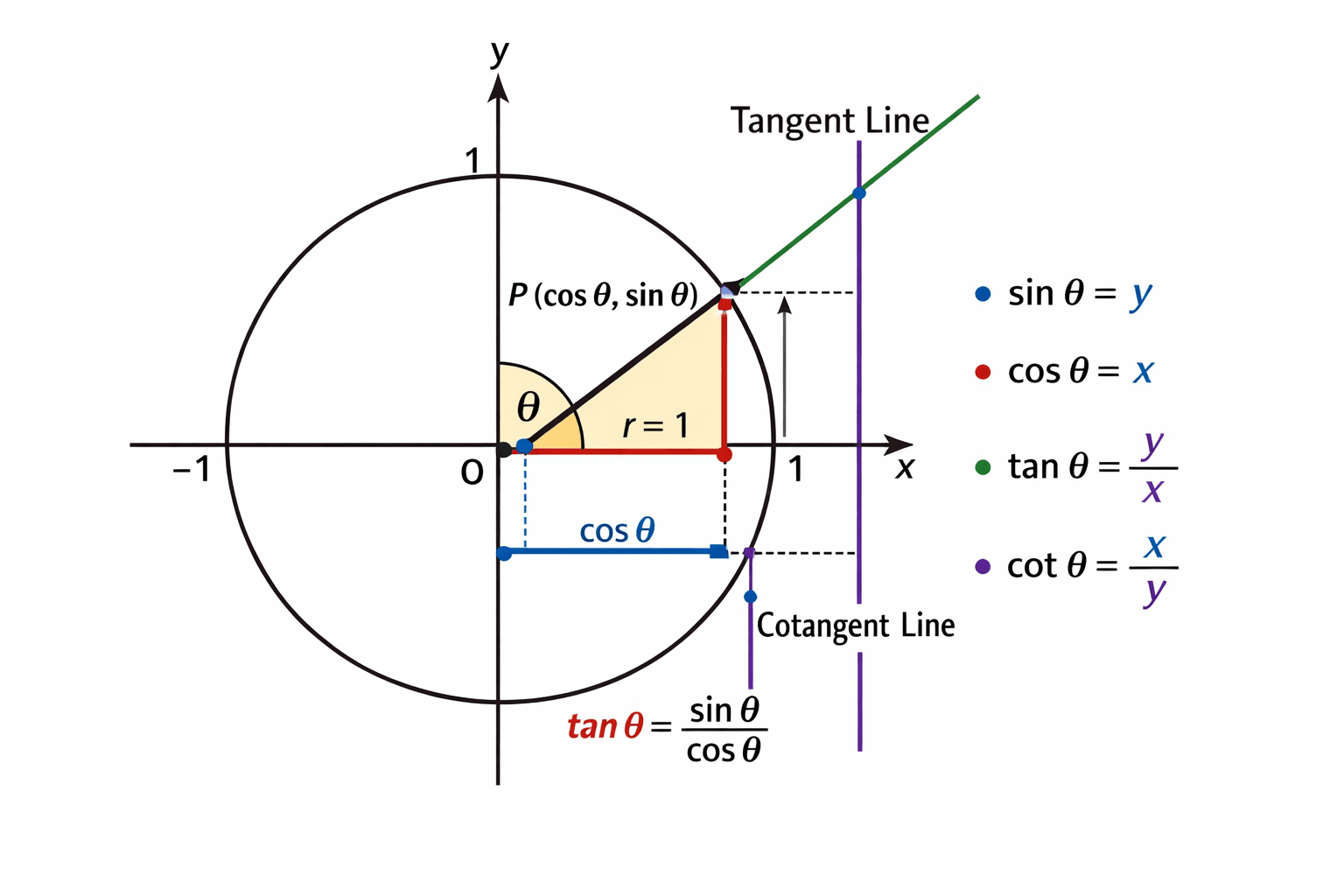
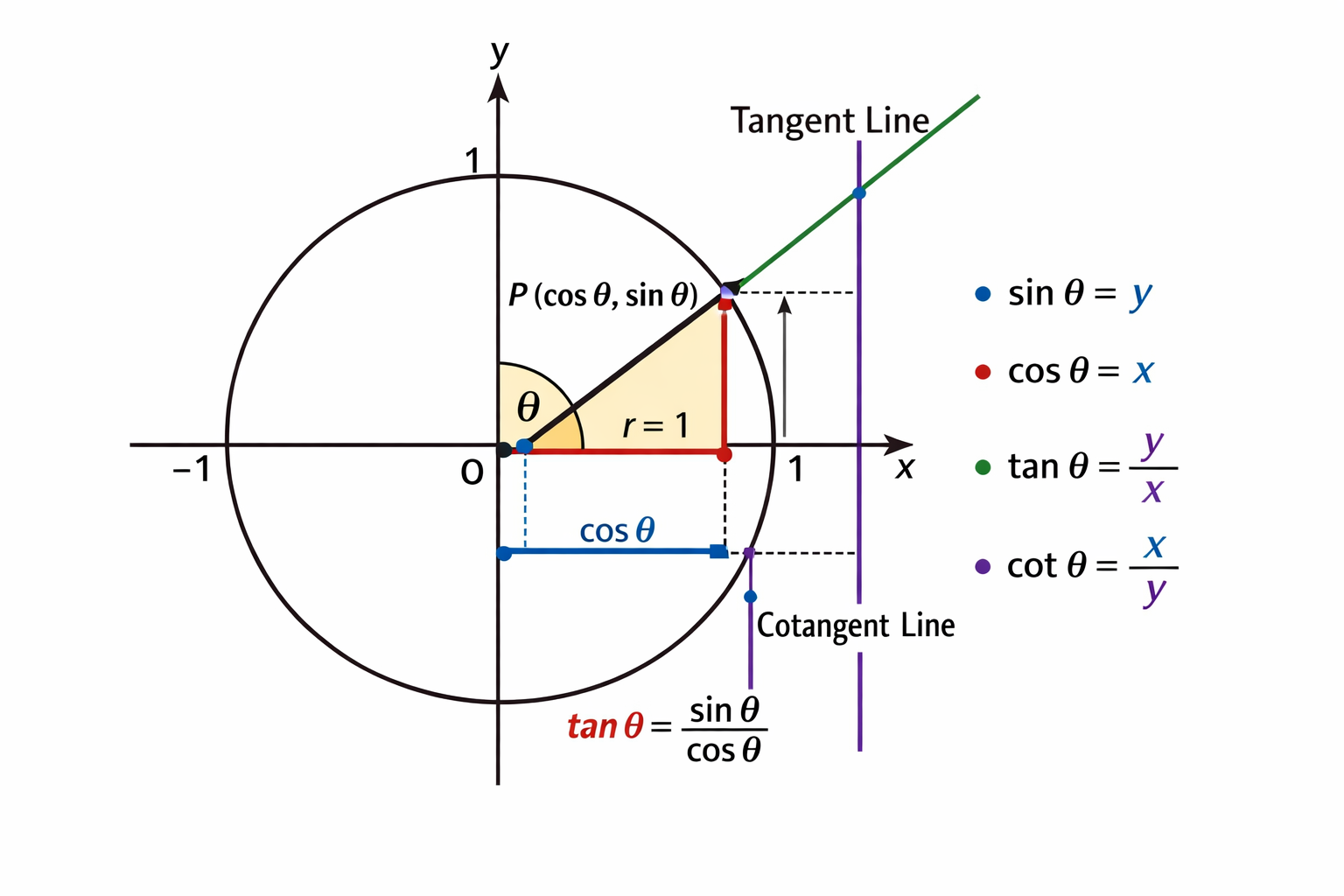
1. دایرهٔ مثلثاتی چیست؟

دایرهٔ مثلثاتی دایره‌ای با شعاع برابر با 1 است که مرکز آن در مبدأ مختصات یعنی O(0,0) قرار دارد.

به این دایره، دایرهٔ واحد یا Unit Circle گفته می‌شود و پایه‌ی تعریف تمام نسبت‌های مثلثاتی است.

هر نقطه روی این دایره را می‌توان با یک زاویه به نام θ (تتا) توصیف کرد.

2. زاویه θ چگونه تعریف می‌شود؟

زاویه θ از محور x مثبت شروع می‌شود و در جهت خلاف عقربه‌های ساعت دوران می‌کند.

این دوران تا شعاعی ادامه پیدا می‌کند که به نقطه‌ای روی دایرهٔ مثلثاتی برسد.

زاویه θ می‌تواند هر مقداری داشته باشد؛ از جمله 0، 30 درجه، 45 درجه، 90 درجه و حتی زوایای بزرگ‌تر از 360 درجه.

3. نقطه P روی دایرهٔ مثلثاتی

نقطه‌ای که شعاع دایره پس از چرخش زاویه θ به آن می‌رسد، نقطه P نام دارد.

مختصات این نقطه به‌صورت زیر تعریف می‌شود:

P(cos θ , sin θ)

به این معنا که:

• مختصات افقی یا x برابر با cos θ است
• مختصات عمودی یا y برابر با sin θ است

این رابطه، مهم‌ترین مفهوم در دایرهٔ مثلثاتی محسوب می‌شود.

4. سینوس و کسینوس روی دایرهٔ مثلثاتی

در دایرهٔ مثلثاتی، نسبت‌های سینوس و کسینوس مستقیماً از مختصات نقطه P به‌دست می‌آیند.

سینوس (sin θ):

sin θ برابر با فاصلهٔ عمودی نقطه P تا محور x است.

sin θ = y

کسینوس (cos θ):

cos θ برابر با فاصلهٔ افقی نقطه P تا محور y است.

cos θ = x

5. تانژانت (tan θ)

تانژانت نسبت سینوس به کسینوس است و به‌صورت زیر تعریف می‌شود:

tan θ = sin θ / cos θ

از نظر هندسی، تانژانت روی خط مماس بر دایرهٔ مثلثاتی نمایش داده می‌شود.

این خط مماس از نقطهٔ تماس شعاع با دایره عبور می‌کند و طول آن مقدار tan θ را نشان می‌دهد.

زمانی که cos θ = 0 باشد (مانند زاویه 90 درجه)، تانژانت تعریف نمی‌شود.

6. کتانژانت (cot θ)

کتانژانت معکوس تانژانت است و به‌صورت زیر تعریف می‌شود:

cot θ = cos θ / sin θ

کتانژانت روی یک خط مماس عمودی نمایش داده می‌شود و طول آن مقدار cot θ را نشان می‌دهد.

زمانی که sin θ = 0 باشد (مانند زاویه 0 درجه)، کتانژانت تعریف نمی‌شود.

نتیجه‌گیری

دایرهٔ مثلثاتی ابزار اصلی برای تعریف و درک نسبت‌های مثلثاتی است. با شناخت دقیق زاویه θ، نقطه P و ارتباط آن با sin، cos، tan و cot، می‌توان مفاهیم پیشرفته‌تر مثلثات را به‌صورت کاملاً مفهومی یاد گرفت.